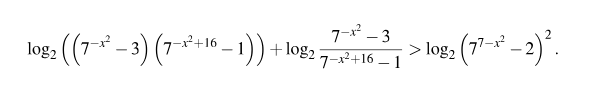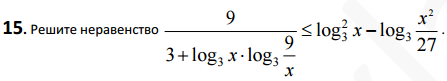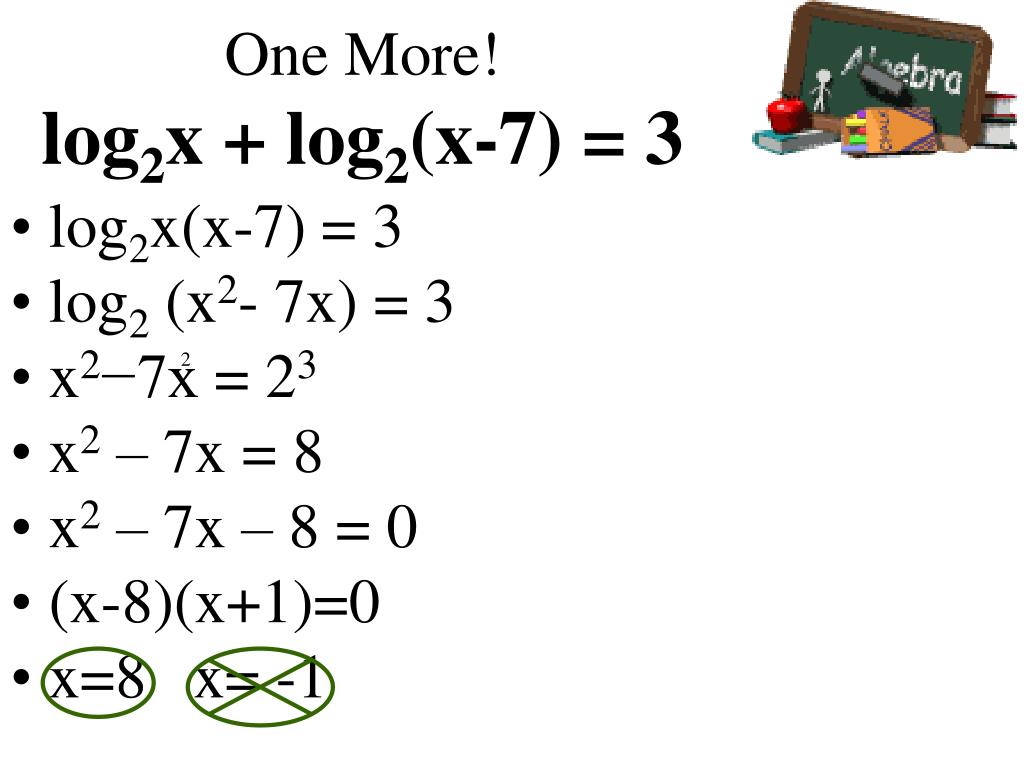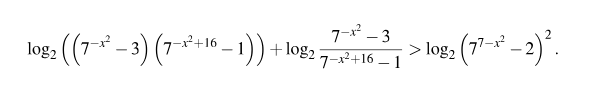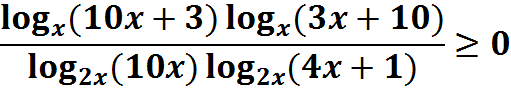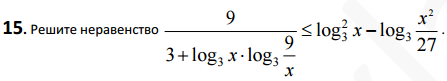Log7(2x-1)=2. Решить уравнение log. Log3 (8x -5)=log311. Log3(x+3x-7)=1. Log2(x+1)=4.
|
2log2 3. Log x2+x x2-2x+1 1. 1 log2 x 1 log2 7x 2 log2 x-1. 3 7 log7 11. Lig по основанию 1/4(2x + 5) больше -2.
|
Log2x. Log2(7-х)=2log8 3. Log2 (x2-x-12) меньше 3. Log 1/2 x. Log2log 2 x^3+8 log 2 x+2 + 2log2 4-x.
|
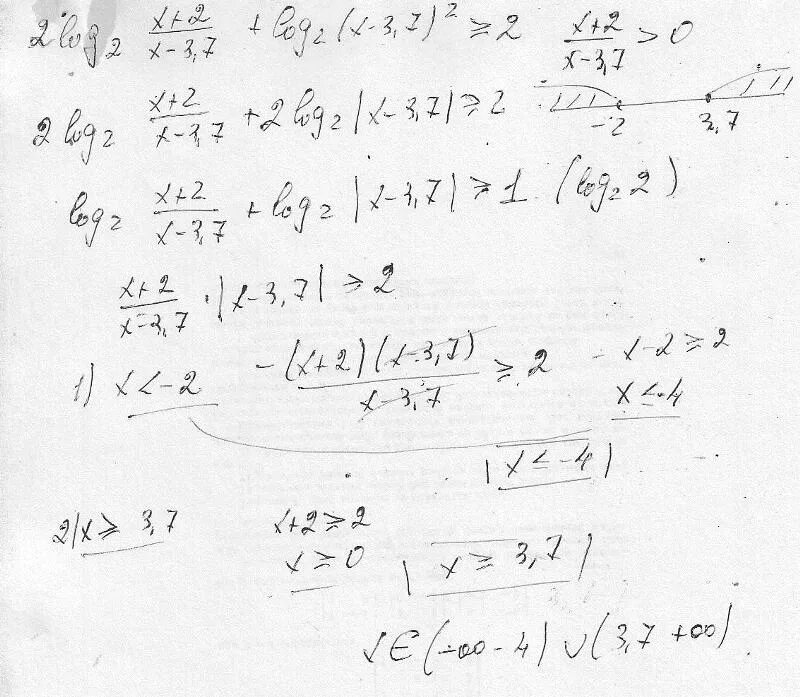Решите неравенство log3(x*x-x-2). Решите неравенство log. Log 2 2 x - log 2 x-2. Решите неравенство log^2. Лог 2/7 -2х+13 -1.
|
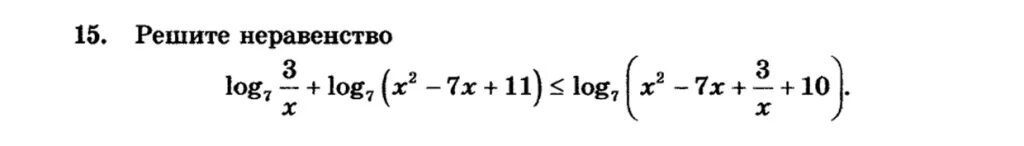Log2(7-х)=2log8 3. 2log2 (2x-2) <= x. Неравенство log7^x^2. Log2 2x 1 больше 4. Log5(x^2-4) log25(х-2)+log25(x+2))⩾2.
|
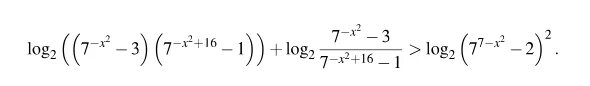Лог 1/7(4x+1) <-2. Log3 x>1 решение неравенства. Log2 7 x 2-3 7 x 2+16-1. Log 2 4+ х log 2 -x +2. X log x 3 2x 7.
|
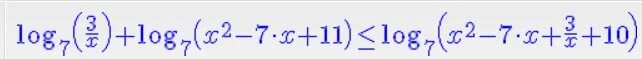Log3 2x 1 log3 13+1. 3. Log2(х+3)=−1. Log3(1-2x)=1. Log3 (4x - 7)=2log3(x-1).
|
Log5(√x2-7x+5)>log1/5(5/√x2-7x+√x+3+2)+1. Log7 2x+5 1. X log x 3 2x 7. X log x 3 2x 7. Log2 x 2 3 log2 x 2.
|
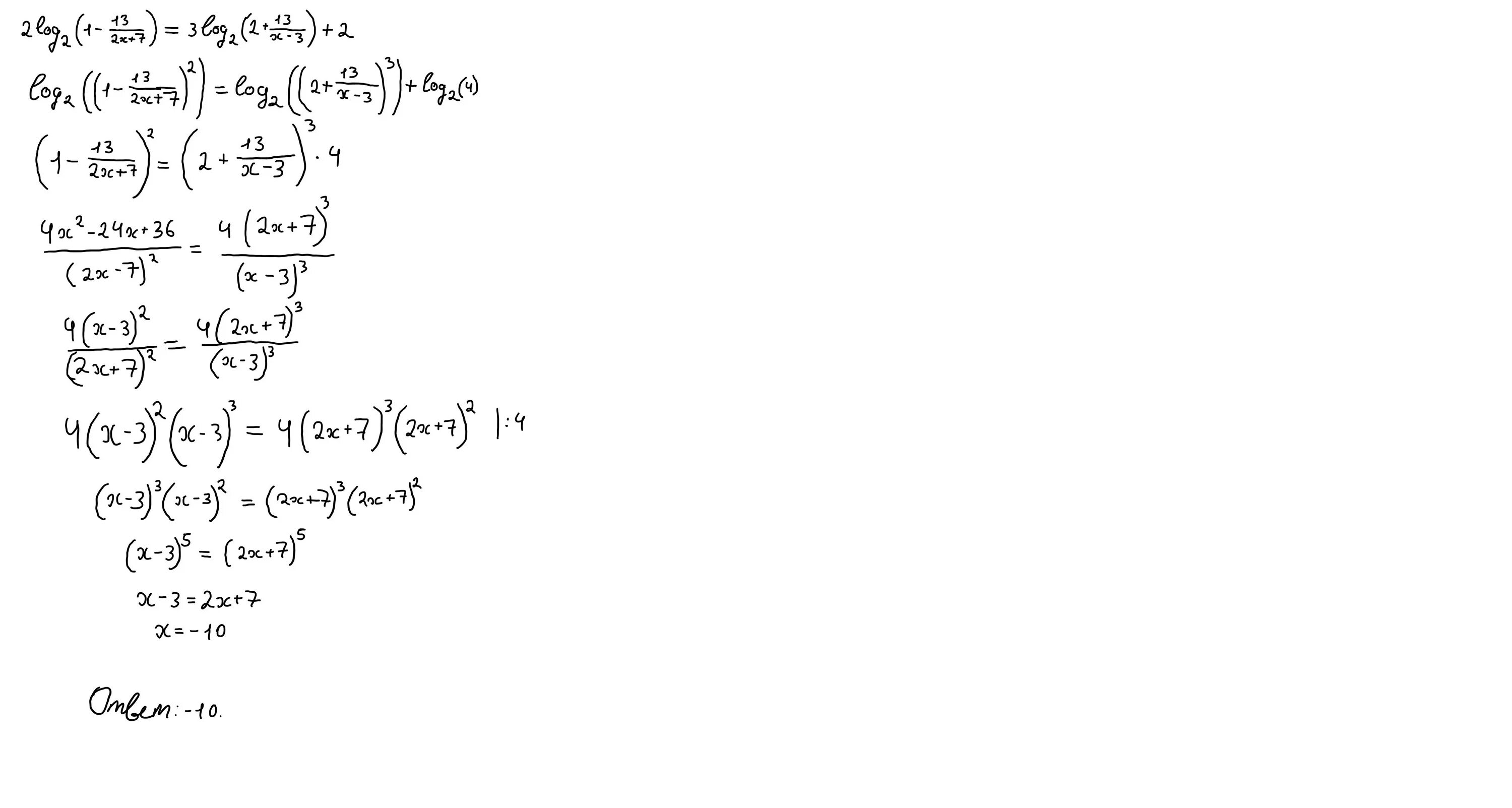Log4 2 x 1 x-1 1. Log3(x+2)+log3x<log3(2x+1). Лог 10 10 = 1. Log 2x-1(9-9/x) производная. X log x 3 2x 7.
|
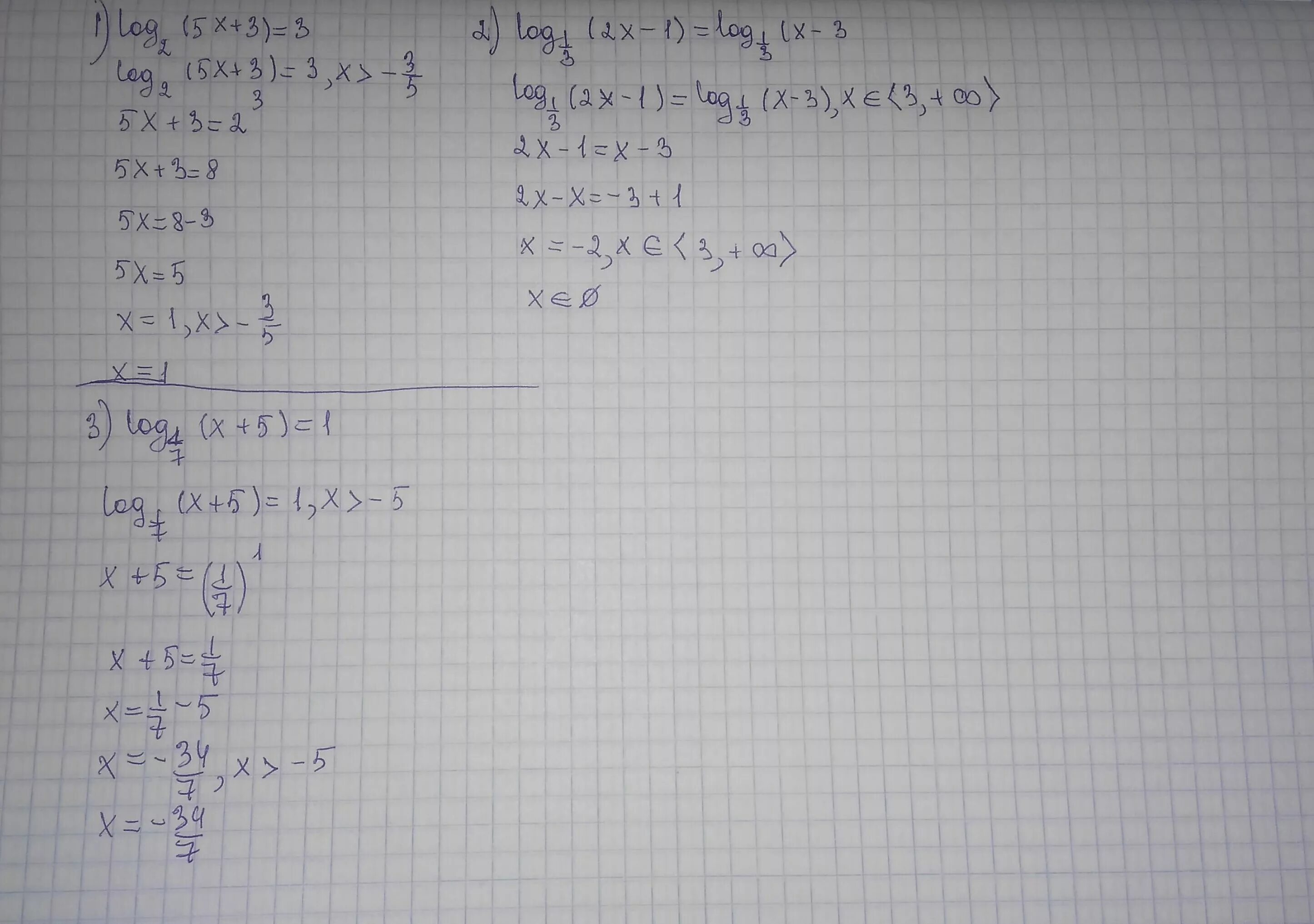X log x 3 2x 7. X log x 3 2x 7. Введение новой переменной логарифмических уравнений. Log x-2 (2x-9)<0. X log x 3 2x 7.
|
X log x 3 2x 7. X log x 3 2x 7. Log10 4. 2log2 x+2/x-3. 2(x-3)=7(2+x).
|
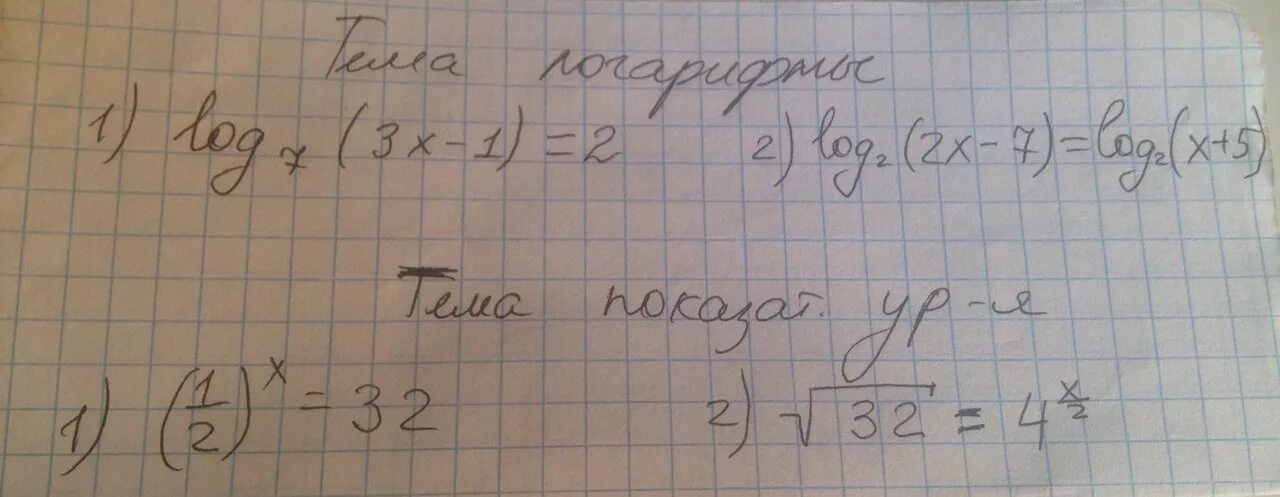Log7x=2. Log2 x больше 0. Log1/3(4х+5)=log1/3(x^2+8x). Log1/10( x-1)+log1/10(x+2)=-1. Логарифмические уравнения log12 (x^2-x)=1.
|
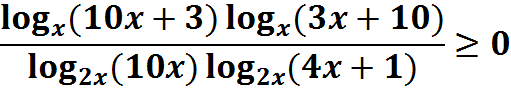Log _(x-1)(2x)>=1. Log1 3 x-1 больше или равно x 2-2x-9. X log x 3 2x 7. Log11(x2-1). X log x 3 2x 7.
|
Log5(3x-7)=log5(x+5). Метод введения новой переменной логарифмические уравнения. Logx=1-x. Решите неравенство log3 (x-7)<3. X log x 3 2x 7.
|
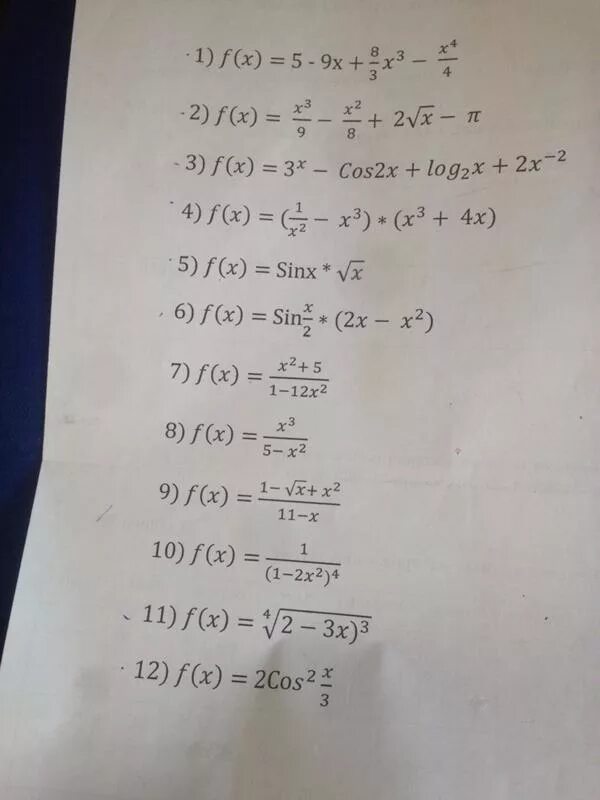Сравнить log1/2 1/3 и log1/3 1/2. X log x 3 2x 7. Log2(7+x)=7. Log ( x ) 7 x–2 =7. X log x 3 2x 7.
|
Log2(x-2)>0. X log x 3 2x 7. Log3(x^2-5x-23)=0. 7. Логарифмические уравнения log2/3 + log3.
|
X log x 3 2x 7. 7/x+8 -1. Log 1/7 7-x -2. Log3^2x=2-log3x. 2 log 2 x +2 x -3.
|
7 log2 x-3. Решите неравенство: log7(2+2x)−log7(x+3)≤log7(6+xx2). X log x 3 2x 7. X log x 3 2x 7. Log3(x-7)<3.
|
X log x 3 2x 7. X2log512 x+7 log2 x2+14x+49. Log2(2^x-7)=3-x. Log 1/2 x. 7 2 2.
|
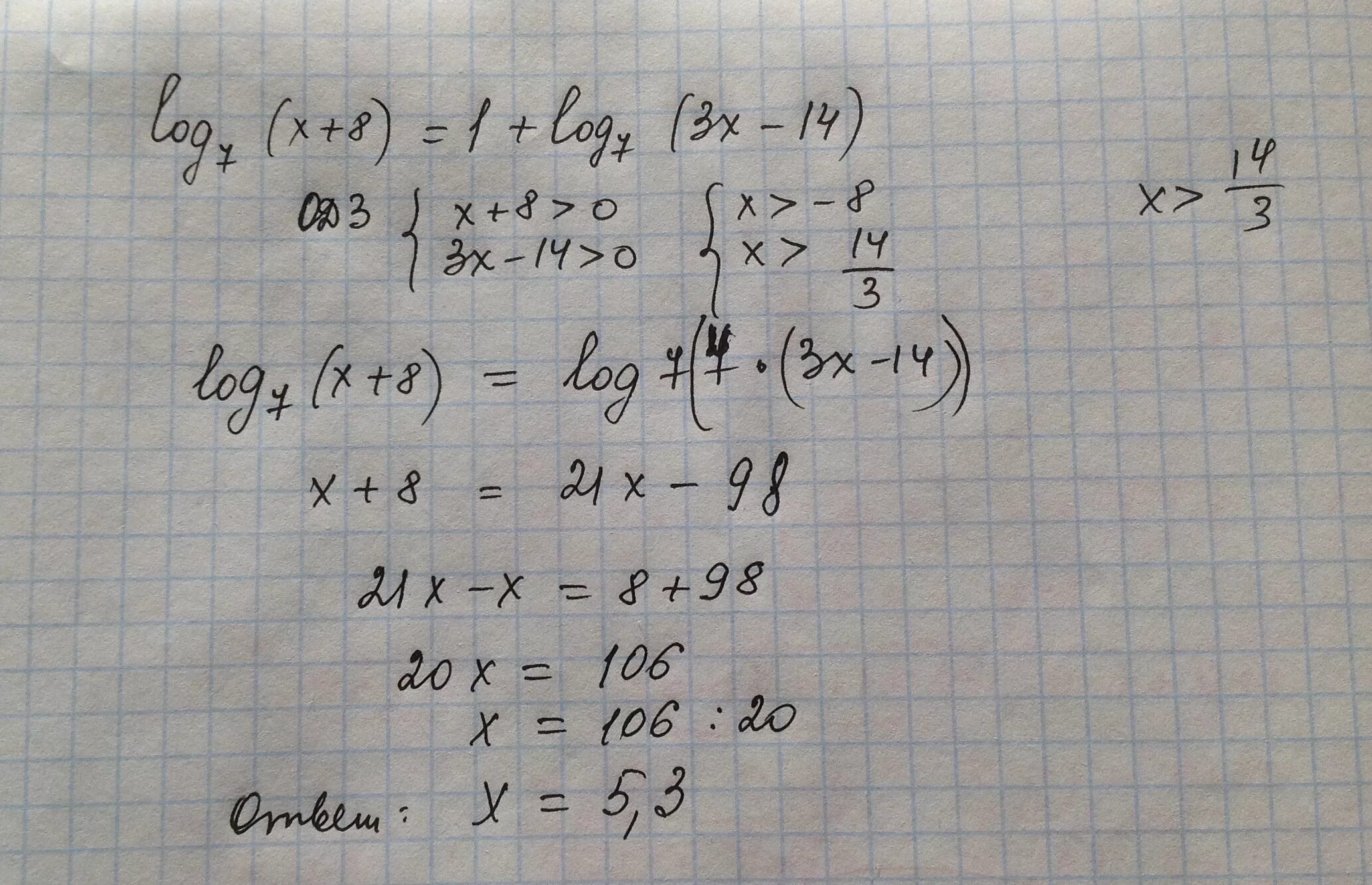Log1/7 7-3x -2. Log2x=3. Log7(x+3)=2. X log x 3 2x 7. Log2(3x-1)-log2(5x+1)<log2(x-1)-2.
|
