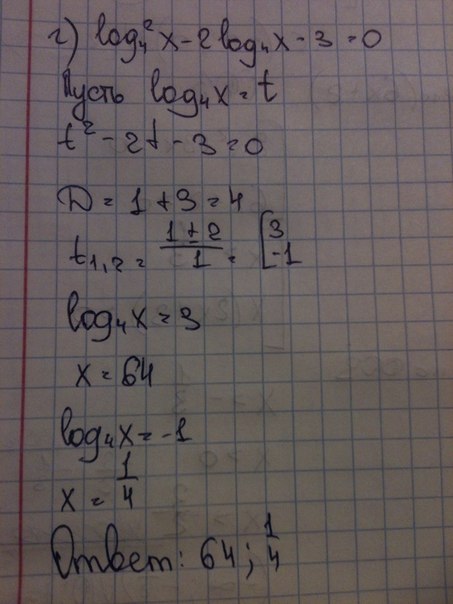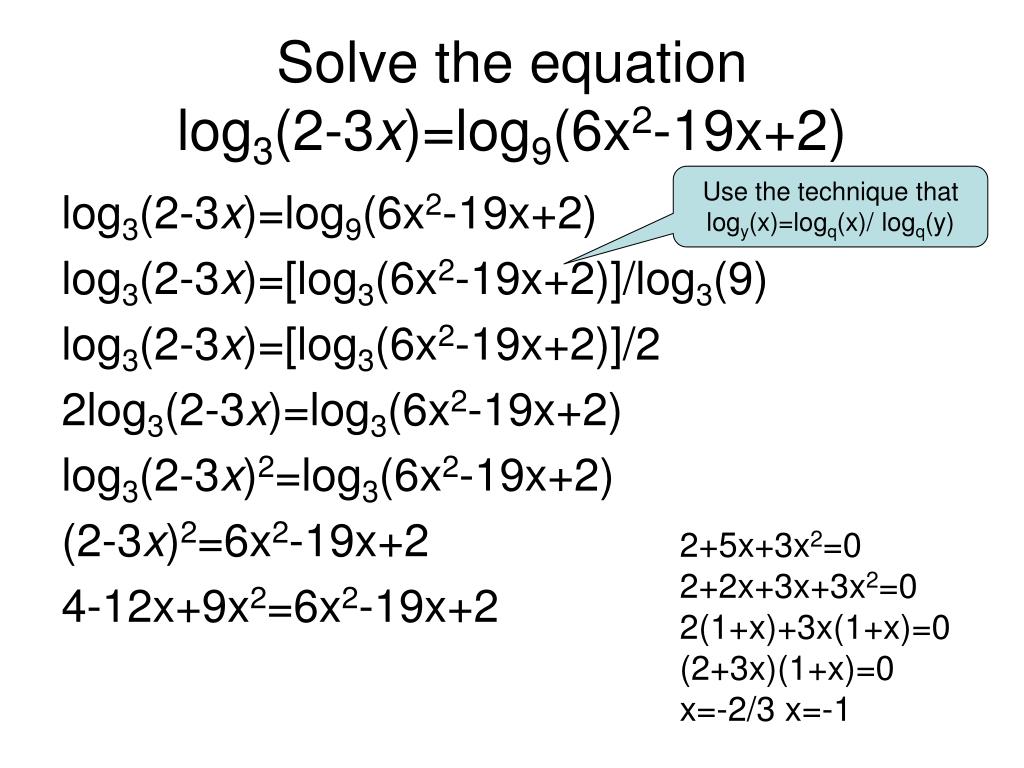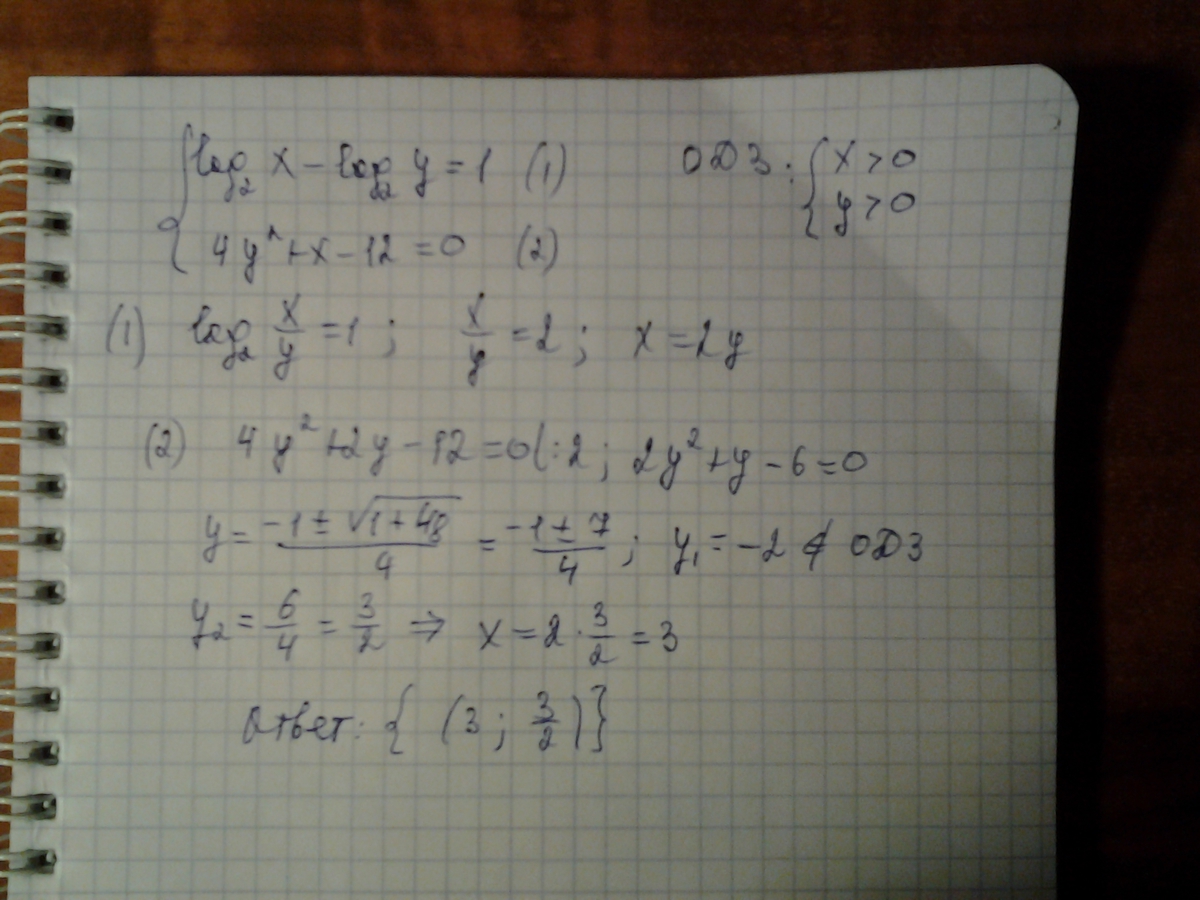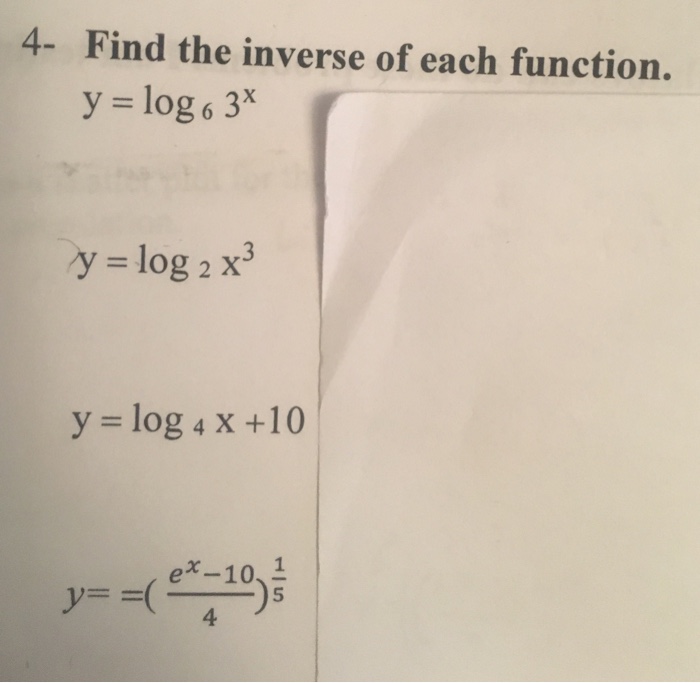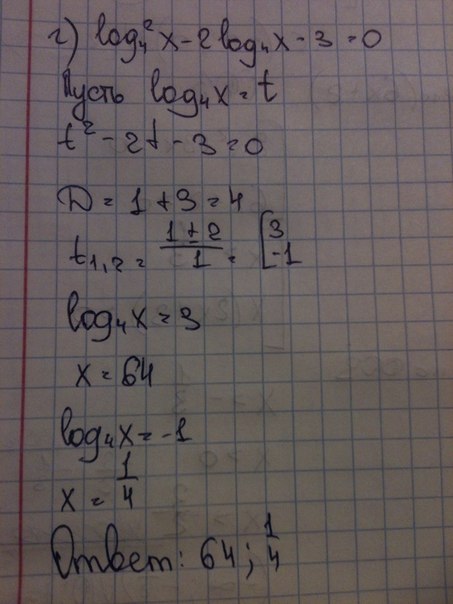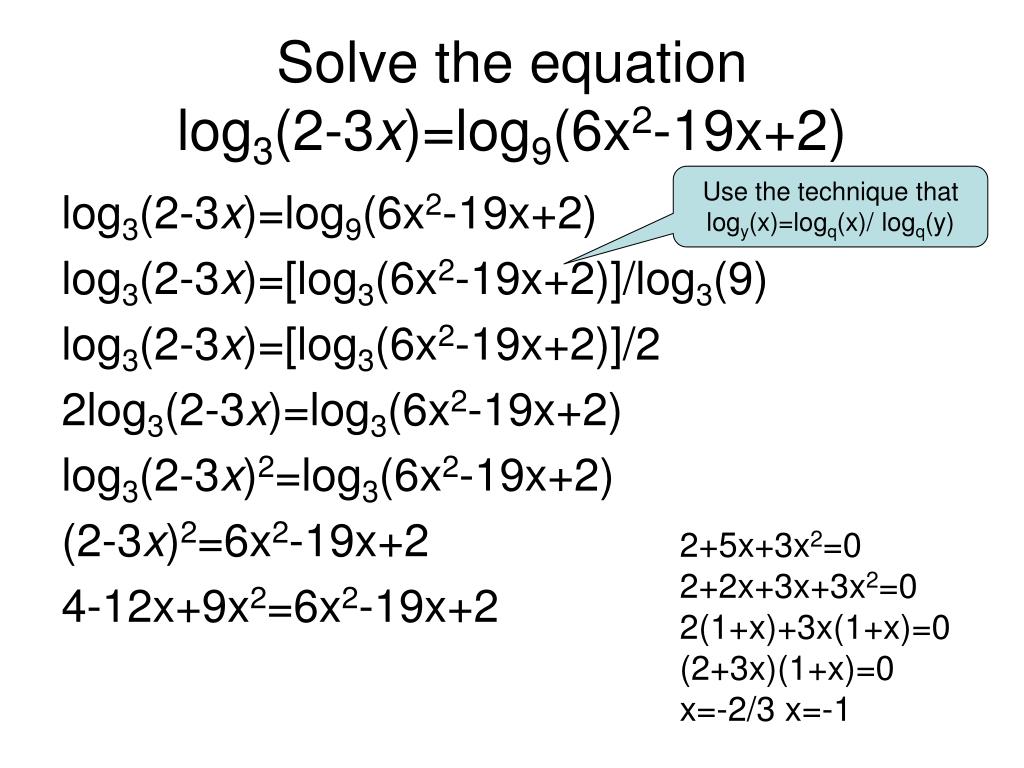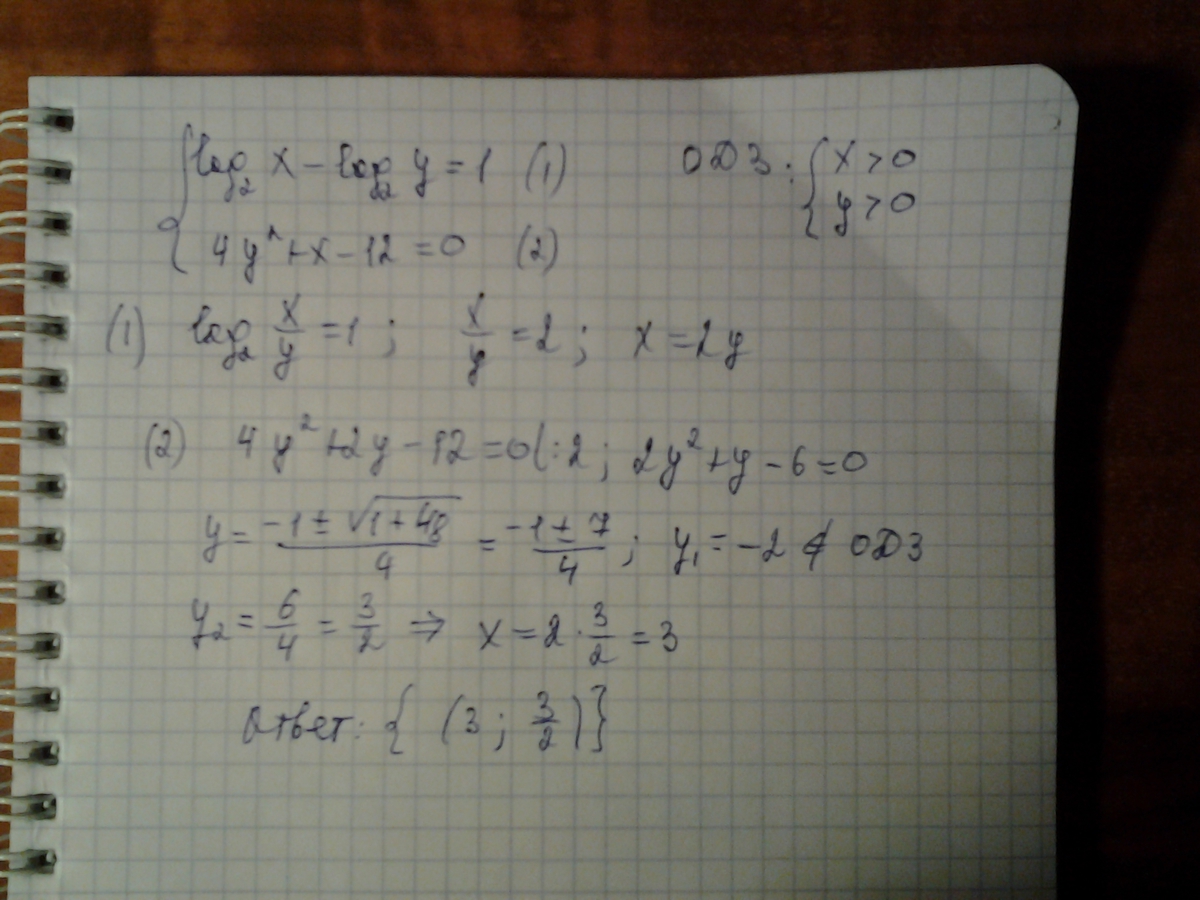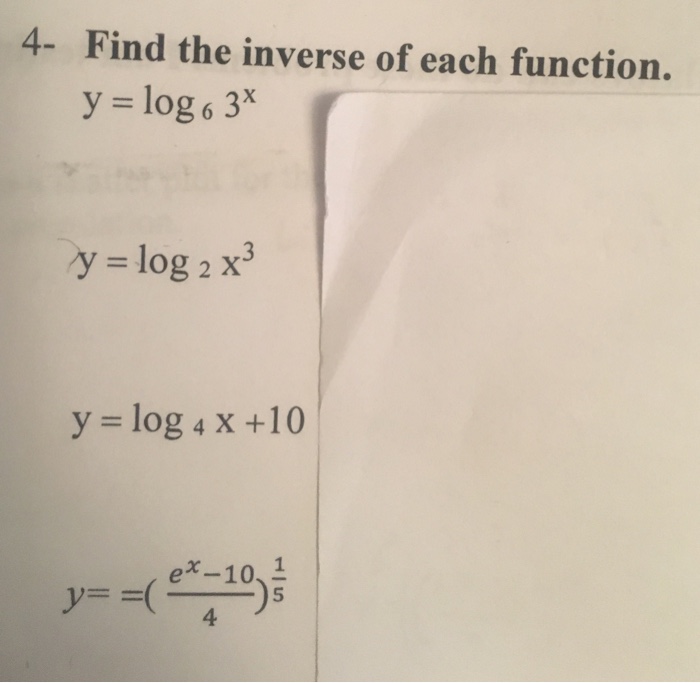Лог 2 10. Система уравнений x+y=3. Решение систем логарифмических уравнений. Log5x=2. Решение уравнения log5(6x-5)=2.
|
5 (3x-1)=-3. Log4(x-2)<2. X^2log625(2-x). Log5 4 x 2 решение. Y log5 x2 6x 12 2.
|
Решите уравнение log3 8+7x log3 (3+x) +1. Системы показательных и логарифмических уравнений. Лог х (х^2 -7х +12)<1. Log2x>1. Одз log(x) < 2 0.
|
Log2x+log2y 5 3x-y 20. Y log5 x2 6x 12 2. Y log5 x2 6x 12 2. Log5 625. Y log5 x2 6x 12 2.
|
X 2log625 6-x log5 x 2-12x+36. Log12 3+log12 4. Y log5 x2 6x 12 2. Log4x=2. Log3 2 log3 2 log2 6 log3 6.
|
Решение системного уравнения { x+2y=3 2x-2y=6. Log2^2x-log2x-2=0. Лог 2 5. 2log4 3x2+2 log2 2x2+5x+2. X2log625(x +2) ≥ log5(x2 + 4x + 4).
|
Y log5 x2 6x 12 2. Y=log2(x+2)-3. Решение log*log. Log2 x + log2 y =2 log3(x-y)=1. Y log5 x2 6x 12 2.
|
Y log5 x2 6x 12 2. Log2 3 х-2 log3 х-3. Логарифм 7 (х+6) = лог 9(6х-9). Log4 2x2+x /log5 2-2x 0. Log 2 4x - x =3.
|
Y log5 x2 6x 12 2. Y log5 x2 6x 12 2. Log2 12. Log2(x-5)+log2(x+2)=3. Как решать систему логарифмических уравнений.
|
Системы логарифмических уравнений. Решите систему x+y 6 log2 3-log2 x. Решить уравнение log0. Y log5 x2 6x 12 2. Log4(x+2)=3.
|
Y log5 x2 6x 12 2. Y log5 x2 6x 12 2. Y log5 x2 6x 12 2. Y log5 x2 6x 12 2. 2log5x log корень x x-log1/5x 8.
|
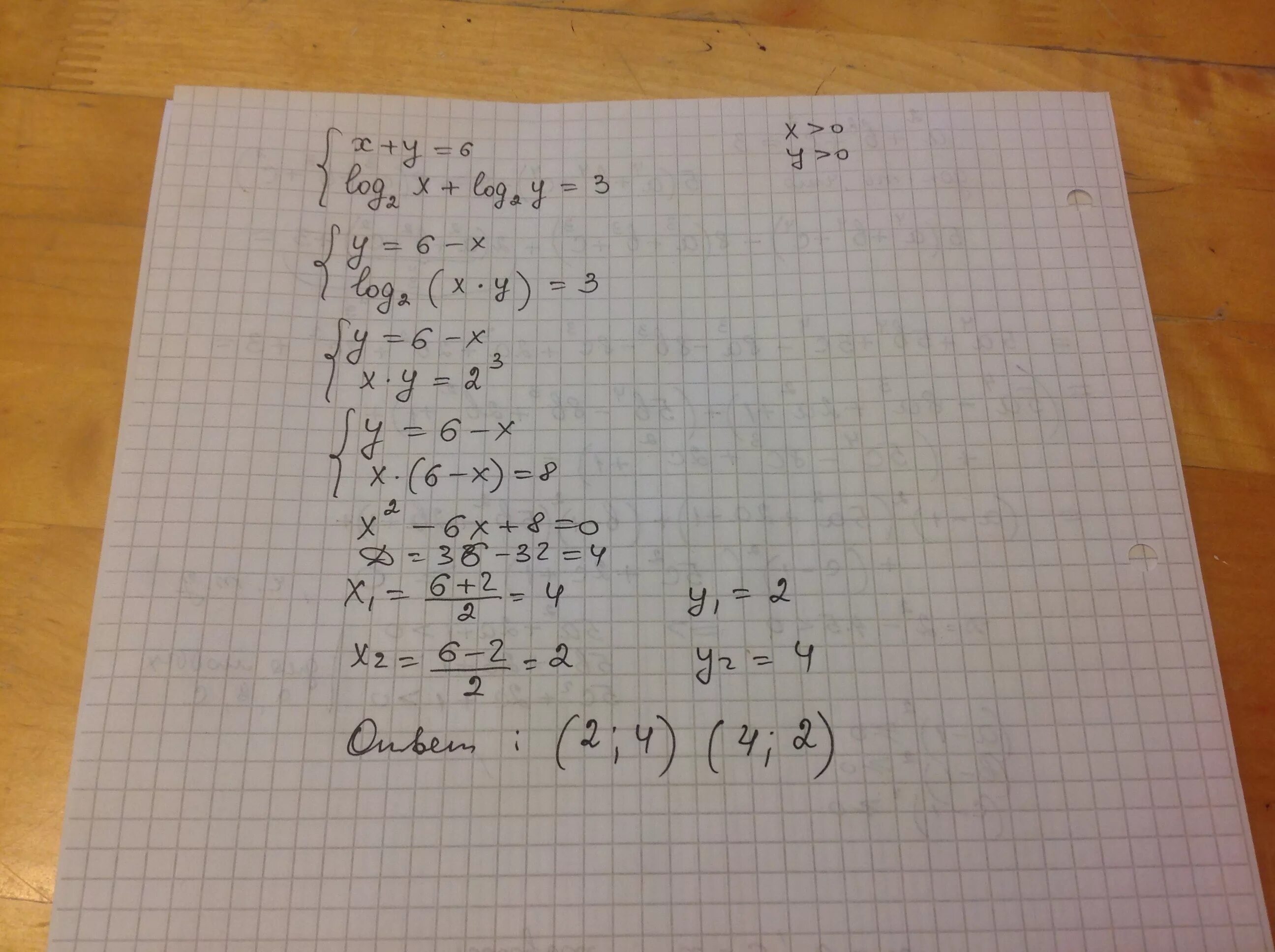1. Log2. Система x+y 6 log 2y 3 - log 2x. Log9 x 7 2 log81 x 3 4+log3 x 3 3x. Y log5 x2 6x 12 2.
|
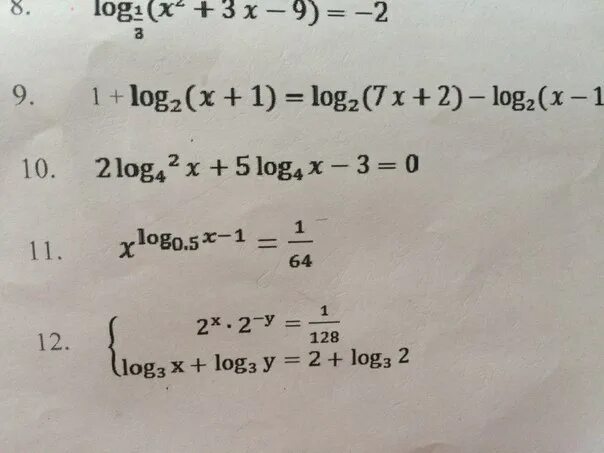Y log5 x2 6x 12 2. Lg4 x2-4 2 log3 x2-4 4. Логарифмы 5. Log1 7 х+7 -2. Log5 125 решение.
|
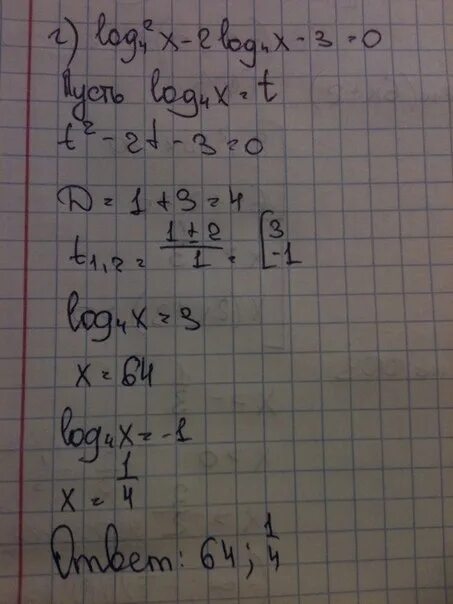Y log5 x2 6x 12 2. Метод введения новой переменной логарифмические уравнения. Log(2-x)(2x^2-5x+2)=2. Log_1/3(x+2)-log_9(x+2)=>-3/2. Log5 5 x 2log5 3.
|
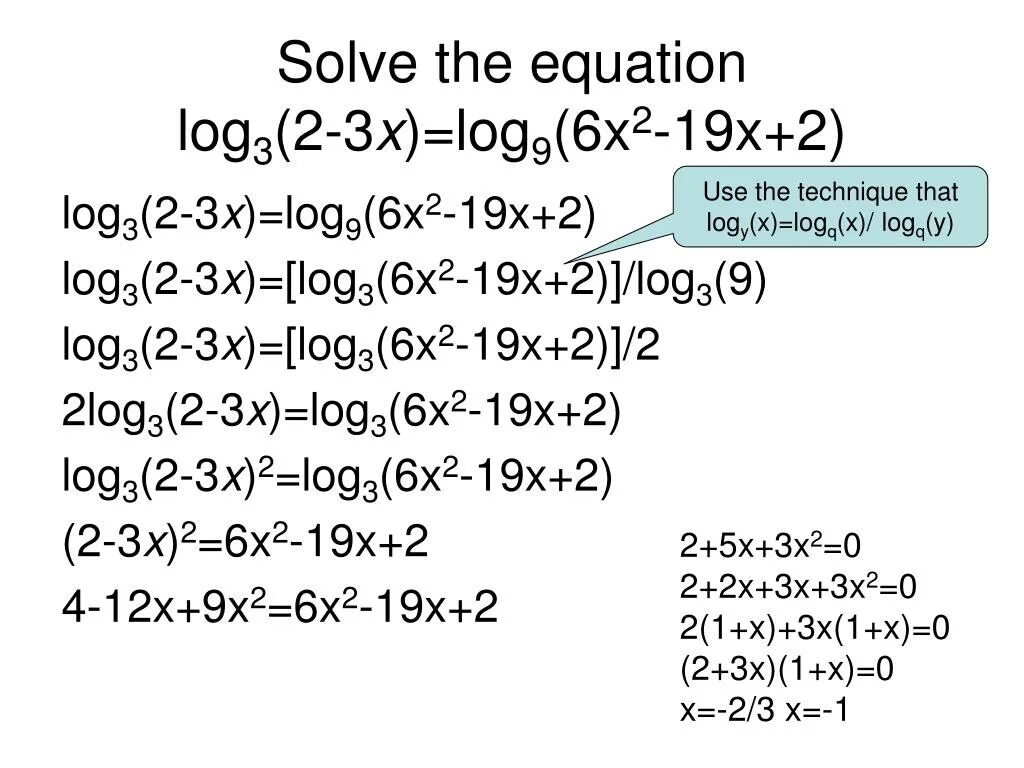Log2(x-2)<2. 1. 1 log 5. Y log5 x2 6x 12 2. Y log5 x2 6x 12 2.
|
Решение уравнения log5(6x-5)=2. 1 log 5. Y log5 x2 6x 12 2. 1 log 5. 5 (3x-1)=-3.
|
Log12 3+log12 4. Log4(x+2)=3. Log2x>1. Y log5 x2 6x 12 2. X 2log625 6-x log5 x 2-12x+36.
|
Y=log2(x+2)-3. Одз log(x) < 2 0. Log5 625. Y log5 x2 6x 12 2. Система уравнений x+y=3.
|
Решение log*log. X2log625(x +2) ≥ log5(x2 + 4x + 4). Y log5 x2 6x 12 2. Решение систем логарифмических уравнений. Y log5 x2 6x 12 2.
|
Метод введения новой переменной логарифмические уравнения. Log5 625. Log9 x 7 2 log81 x 3 4+log3 x 3 3x. Y log5 x2 6x 12 2. Одз log(x) < 2 0.
|
